What is a Function?

Written By Emma Gardiner

A function is one of the most fundamental concepts in calculus. Here is the most basic one:

y = f(x)

In algebra, students are often taught to use methods such as substitution and elimination to solve equations like y = x + 4. In calculus, you will see functions that are very similar except that you will commonly see them written using f(x):

f(x) = x +4

How Does a Function Work?

Think of a function like a machine that you put a certain number into. The machine then gives you a different number based on the number you put in.

For example, say you have a machine that adds 1 to any number that you put in. If you put a 1 into it, the machine will give you a 2. If you put a 53 into it, you will get a 54. We could write this function like this:

y = f(x + 1)

The x represents the number that you put into the machine, and the y represents the number that the machine gives you. The y value will change depending on the number that you put into the machine (the x value). For this reason, we call the y value the dependent value, and the x number is the independent value.

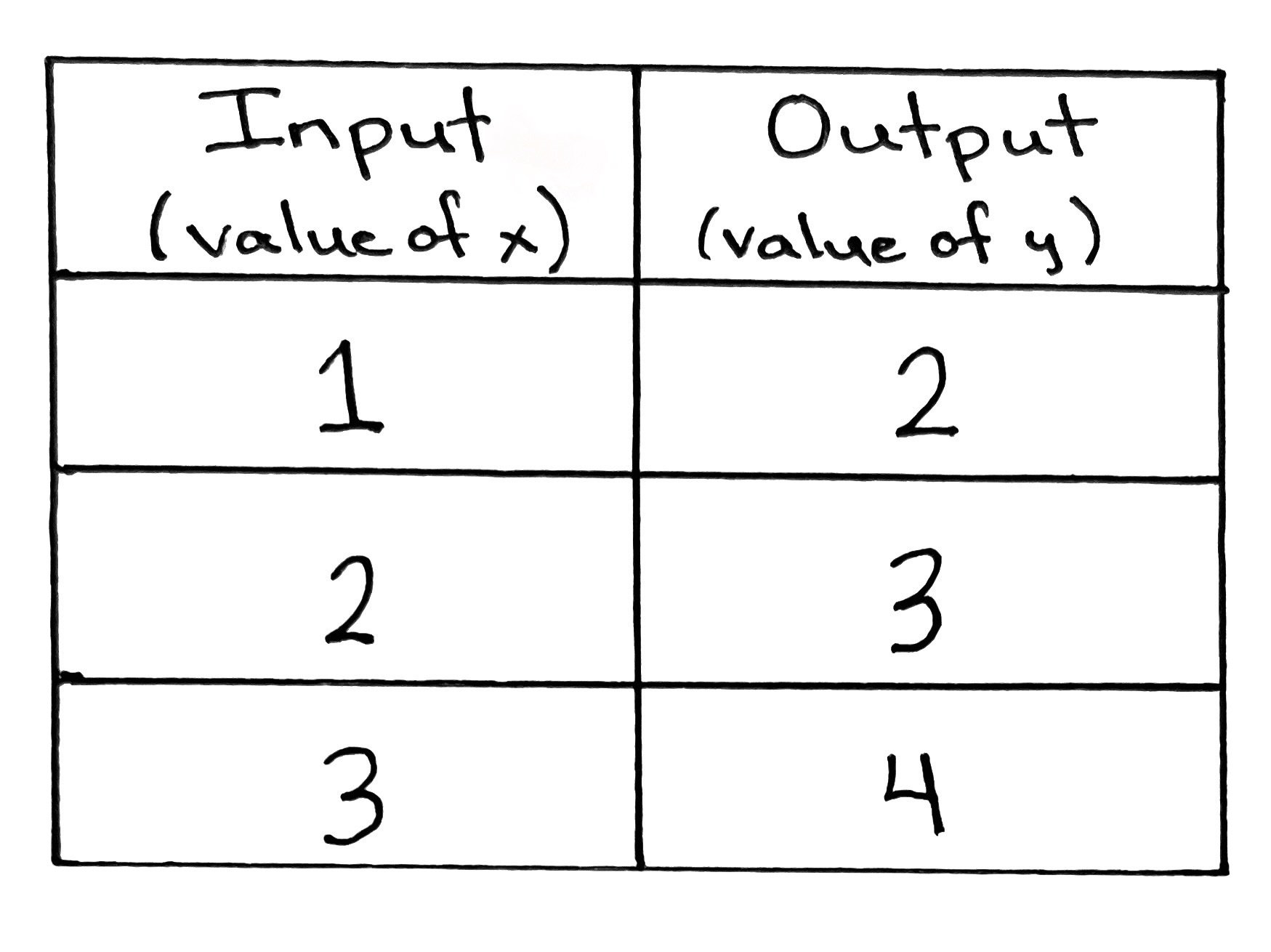
We can also illustrate this function using an input/output table. Using the example of a function that adds one to the number you put in, y = f(x +1), the numbers would look like this:

 
 

The first column represents all the numbers you put into the machine. These are the x values of your function. The second column (on the right) is all the numbers that the machine will give you after adding 1. These are the y values of your function.

How to Solve a Function for y

To solve a function for its y value, input a given number into the function. We do this by replacing all the values of x in the function with the number given to us in the question.

Here’s an example:

Vertical Line Test

In order to test whether a given equation is a function, use the Vertical Line Test. Graph the function (see our lesson on how to graph functions here) or if provided, look at the graph of the function, and draw a vertical line through it. Look for areas where the line touches parts of the graph. Does the vertical line only touch the graph once?

 
 

In the image above, we drew a vertical line through the graph. Because the pink line only intersects the graph once, this is a function.

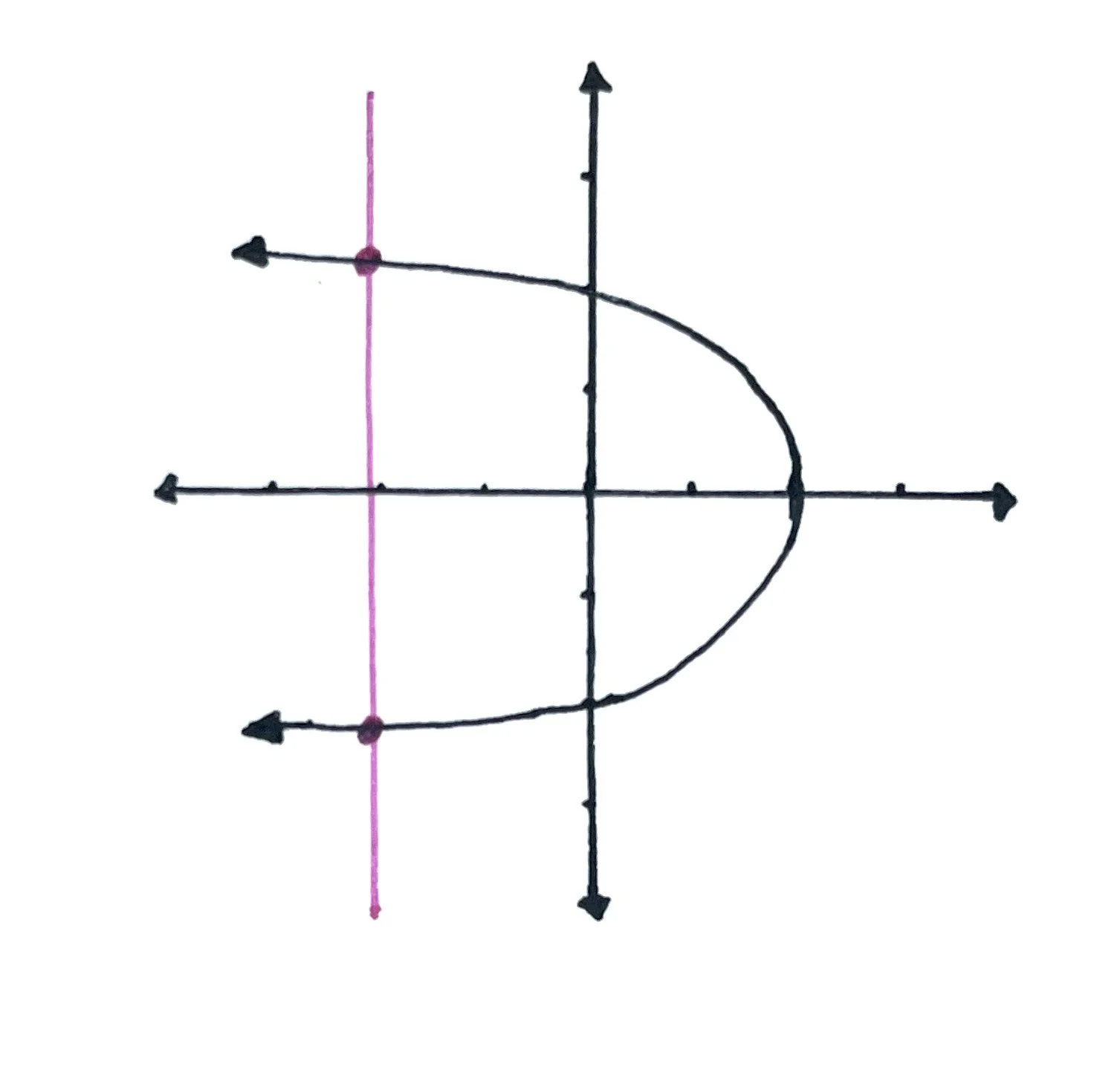
However, if the vertical line touches the graph more than once, it is not a function. Here’s an example:

 
 

In this example, the pink vertical line intersects the graph twice so I know that this graph does not represent a function.

Why does the Vertical Line Test work? In a function, there can only be one value of y for each value of x. If you plug a 2 into your function machine, you cannot get both a 1 and a 3 from it. You can only get one value. For example, perhaps if you plug a 2 into the function machine, you get a 4 and nothing else. That would be a function. So, when a function is represented on a coordinate plane, the curve cannot intersect a value of y twice at the same point of x, as it does in the image above.

Key Points to Remember:

  • A function is an equation where one variable depends on the value of another variable.

  • y = f(x) so if you are asked to solve for f(x), you are solving for the y value.

  • To solve for y, input the given value of x into the function and solve.

  • To test whether something is a function, use the vertical line test on the graph of that function. Check to see if the vertical line intersects the graph more than once. If so, it’s not a function.

Additional Resources

Emma Gardiner
Next

Graphing Functions